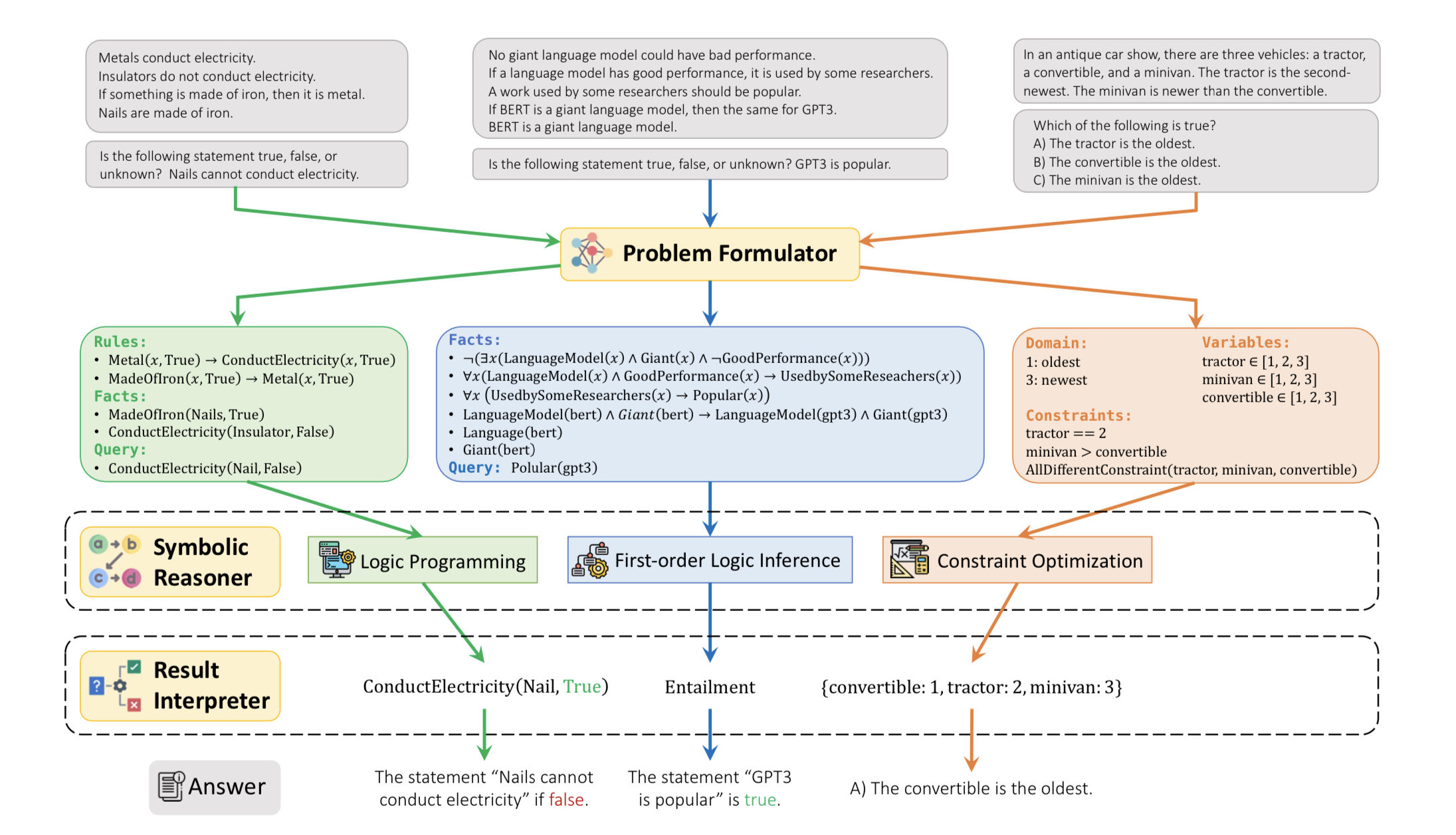
Today we’re going to dive into a fascinating paper called “LOGIC-LM: Empowering Large Language Models with Symbolic Solvers for Faithful Logical Reasoning.”
The authors of this paper claim that Large Language Models (LLMs) often struggle when faced with complex logical reasoning problems. Well, LLMs primarily rely on a chain of thought process, which can be limiting when it comes to intricate logical reasoning. To address this limitation, the authors introduce the concept of logic to enhance LLM performance. They harness the translation skills of LLMs by training them to convert reasoning prompts into symbolic representations using a few-shot generalization technique. They name this process as the problem formulator. This formulator transforms the problem into one of three types: logic programming (modus ponens), first-order reasoning, or constraint satisfaction problem.
Once they’ve converted the problem into a symbolic representation, the authors employ standard methods to solve logic or constraint satisfaction problems. For first-order logic, they use the inference engine from CS221 at Stanford (a course that I recently completed :). To refine the logical form of equations, they’ve built a self-refiner that takes error messages from the solver as feedback, helping them modify any inaccurate representations.
Now, you might be wondering, how do they translate the results back into natural language? Well, they’ve developed something called a result interpreter that converts the solution into an answer we humans can understand. Let’s break it down with a couple of examples to make things more tangible. Take this prompt for first-order reasoning:
Prompt: A Japanese game company created the game The Legend of Zelda. All games in the Top 10 list are made by Japanese game companies. If a game sells more than one million copies, then it will be selected for the Top 10 list. The Legend of Zelda sold more than one million copies.
Question: Based on the given information, is the following statement true, false, or uncertain? The Legend of Zelda is in the Top 10 list.
(A) True
(B) False
(C) Uncertain

According to the model, the answer is True. Now, let’s try to understand how the machine processes this information.
In the realm of first-order reasoning, we create relations that apply to “all” or “at least one.” These relations are indicated by “for all” or “there exists,” allowing us to reason in various ways. The rest is pretty straightforward, with logical operators like “and,” “or,” and “implies” to connect the dots.
So if I were to say 3 statements:
- All human are smart
- John is human
- Sagar is not human
The first order resolution will give us that “John is smart”, given john implies human and human implies smart. However note that this will not give us “Sagar is not smart”.
Now, let’s move on to another example involving Constraint Satisfaction Problems (CSP):
Prompt: The following paragraphs describe a set of five objects arranged in a fixed order. The statements are logically consistent within each paragraph. In a golf tournament, there were five golfers: Rob, Eve, Eli, Amy, and Dan. Dan finished second. Amy finished below Eve. Dan finished above Eve. Amy finished above Eli.
Question: Which of the following statements is true?
(A) Rob finished third
(B) Eve finished third
(C) Eli finished third
(D) Amy finished third
(E) Dan finished third
When I tested this prompt, ChatGPT indicated that all the statements were false. However, we know that statement B, “Eve finished third,” is actually true. Let’s take a closer look at the structure of this problem.
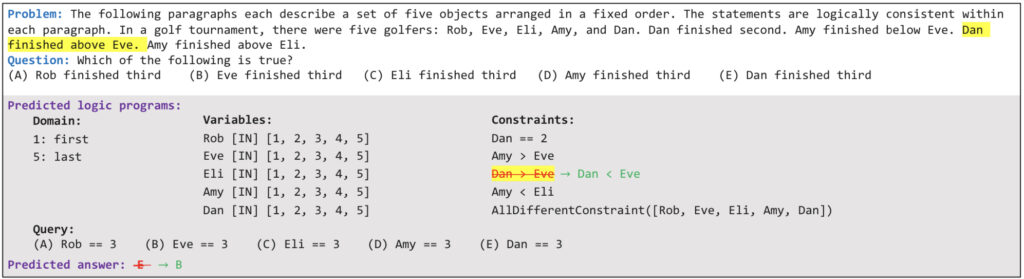
For Constraint Satisfaction Problems (CSP), the formulation is a bit different. In this case, the problem formulator made an error (as highlighted in yellow in the paper). However, it’s pretty obvious that the model will still be able to solve this particular problem.
Now, let’s see the results of various reasoning-based datasets tested with this new logic-enhanced approach.
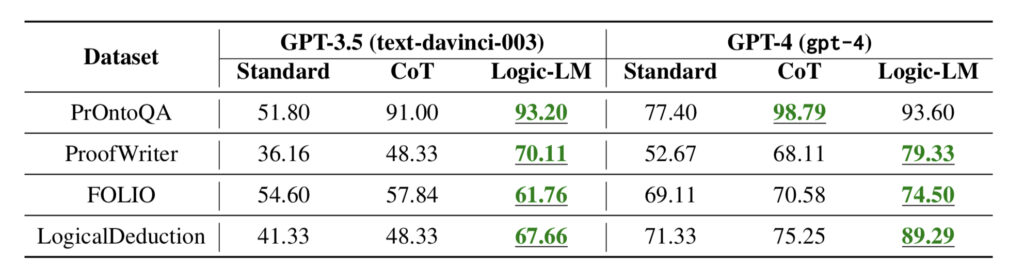
In the image, you’ll find a comparison between the standard LLM, the chain of thought prompting (CoT) approach, and the new logic-LM method proposed in this paper.
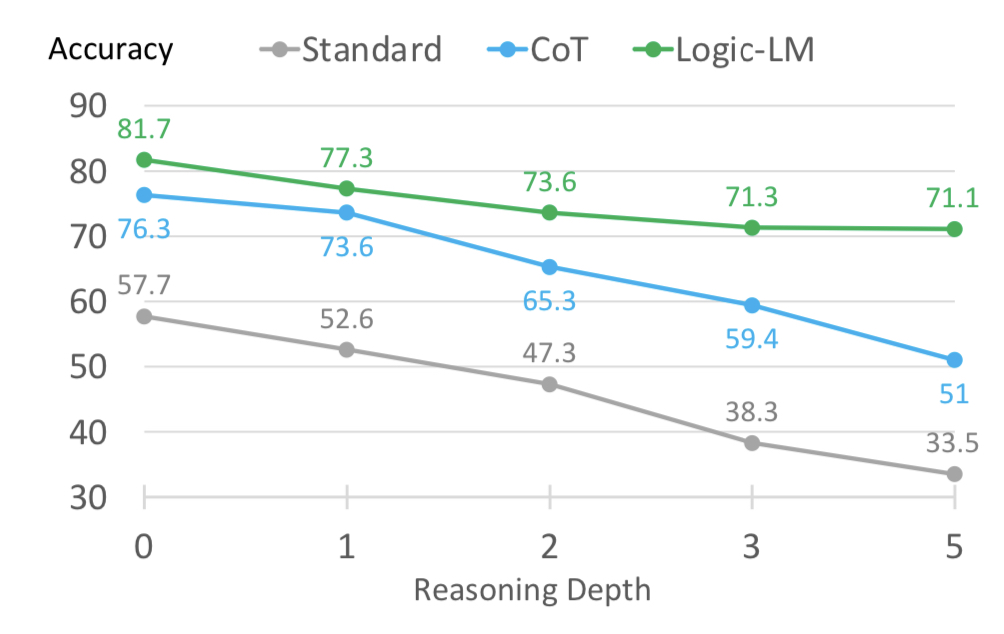
One interesting observation in the result is LogicLM maintains higher accuracy when there is deeper reasoning depth in the prompt, as shown above.
If you’re interested in diving deeper into the details, you can find the full paper here.
And there you have it, a brief overview of the “LOGIC-LM” paper that explores how symbolic solvers can empower large language models to tackle logical reasoning challenges. This has been a super interesting read for me – hope you all like it too.